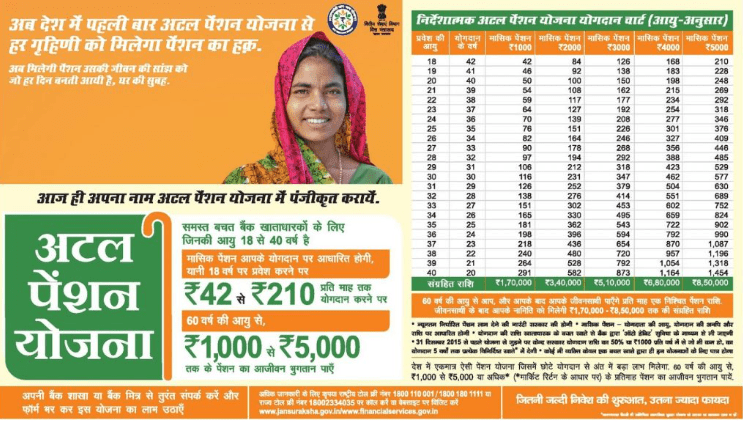
Vestige Product Catalogue April 2023 PDF
Vestige Product Catalogue April 2023 PDF download link is available below in the article, download the PDF of Vestige Product Catalogue April 2023 using the direct link given at the bottom of the content.
Vestige Product Catalogue April 2023 PDF
Vestige Product Catalogue April 2023 PDF Download for free using the direct download link given at the bottom of this article. If you’re in search of high-quality wellness and health products, you should check out the Vestige Products Catalog in April 2023.

Vestige is a well-known brand that provides an extensive range of wellness and health products that cater to various needs. Here, we’ll delve deeper into the Vestige Products Catalog and its advantages. We’ll discuss some of the top products you should try out.
What is Vestige Products Catalog?
Vestige Products Catalog is a comprehensive catalog that features various wellness and health products from the Vestige brand. This catalog includes a broad range of products that cater to different needs and requirements. Whether you’re looking for nutritional supplements, personal care products, or home care products, you can find them all in the Vestige Products Catalog.
One of the benefits of using Vestige products is that they are made from natural ingredients. This means that you don’t have to worry about harmful chemicals that can damage your health. Vestige products are known for their effectiveness, and they cater to different needs.
Top Products in Vestige Products Catalog
- Vestige Flax Oil Capsules – These capsules are a rich source of Omega-3 fatty acids that help to reduce inflammation, support heart health, and improve brain function.
- Vestige Calcium Tablets – These tablets are enriched with Calcium and Vitamin D, which help to strengthen bones and prevent osteoporosis.
- Vestige Noni Capsules – Noni is a natural antioxidant that helps to reduce inflammation, boost immunity, and improve digestion.
- Vestige Assure Natural Herbal Mosquito Repellent – It is made from natural ingredients like Lemongrass, Neem, and Citronella that repel mosquitoes naturally.
- Vestige Assure Hand Sanitizer – It is made from natural ingredients like Aloe Vera and Tea Tree oil that help to moisturize and protect your hands.
The Vestige Products Catalog offers a wide range of wellness and health products that are made from natural ingredients. Their products are safe and effective for your health and cater to different needs. Additionally, Vestige products are affordable and offer value for money. You don’t have to compromise on quality to enjoy affordable wellness and health products.
Vestige Products List April 2023 with Price
| Vestige Healthcare (Vestige Prime) | |
| Combiotics | 525.00/- |
| Sea Buckthorn | 1000.00/- |
| Krill Oil | 1435.00/- |
| Concentrated Mineral Drops (CMD) | 1100.00/- |
| Multi Vita + Min Gummies | 825.00/- |
| Energy Booster | 1050.00/- |
| Absorvit Multivitamin Sublingual Spray | 625.00/- |
| Absorvit Vitamin B12 Sublingual Spray | 625.00/- |
| Absorvit Vitamin C Sublingual Spray | 560.00/- |
| Absorvit Vitamin D Sublingual Spray | 560.00/- |
| Vestige AYURVEDIC PROPRIETARY MEDICINE | |
| SPIRULINA^ | 421.00/- |
| ALOE VERA^ | 320.00/- |
| AMLA^ | 220.00/- |
| NONI^ | 585.00/- |
| COLOSTRUM^ | 720.00/- |
| FLAX OIL^ | 635.00/- |
| GANODERMA^ | 920.00/- |
| Curcumin Plus^ | 1050.00/- |
| HEALTH DROPS panch tulsi ark | 210.00/- |
| NEEM^ | 425.00/- |
| Shatavari Max^ | 545.00/- |
| GLUCO HEALTH^ | 795.00/- |
| VITAL COMPLEX^ | 895.00/- |
| PROCARD^ | 960.00/- |
| RESPOCARE^ | 730.00/- |
| KIDNEYHEALTH^ | 760.00/- |
| LIVERHEALTH^ | 765.00/- |
| TOXCLEAN^ | 825.00/- |
| PROSTATE CARE^ | 525.00/- |
| Vestige HEALTH SUPPLEMENTS | |
| PROTEIN POWDER (200g) | 1050.00/- |
| FOLIC & IRON PLUS | 280.00/- |
| NUTRITIONAL PROTEIN POWDER (200g) | 640.00/- |
| STEVIA | 160.00/- |
| DETOX FOOT PATCHES | 1400.00/- |
| Veslim Shake | 1750.00/- |
| CALCIUM | 270.00/- |
| U-CONTROL | 1600.00/- |
| Vestige NUTRACEUTICALS | |
| COENZYME Q10 | 1160.00/- |
| L-ARGININE | 1515.00/- |
| Veslim | 1290.00/- |
| HMB | 1875.00/- |
| Veslim Tea | 795.00/- |
| PRE GLUCO HEALTH | 1020.00/- |
| GLUCOSAMINE | 610.00/- |
| Collagen | 700.00/- |
| Eye Support | 625.00/- |
| FIBRE | 1000.00/- |
| MELATONIN ORAL SPRAY | 460.00/- |
| HER OWN | 460.00/- |
| HAIR, SKIN & NAIL | 585.00/- |
| Cranberry | 1875.00/- |
| Vestige Health Food | |
| RICE BRAN OIL (2L) | 560.00/- |
| FRESHnUP Drink (200g) | 235.00/- |
| Hi-Nutrition Breakfast Cereal (350g) | 350.00/- |
| SPECIAL TEA (250g) | 160.00/- |
| PREMIUM COFFEE (50g) | 205.00/- |
| PREMIUM SPICE TEA (200g) | 285.00/- |
| PROTEIN SNACK BAR (30g) | 65.00/- |
| CHOCO-FLAXSEED BAR (30g) | 60.00/- |
| ENERGY SNACK BAR (30g) | 60.00/- |
| Vestige Natural Personal Care | |
| SUNSCREEN SPF 40+ | 510.00/- |
| HAIR MASK | 425.00/- |
| LIGHTENING CREAM SPF 15 | 425.00/- |
| FACE SCRUB | 310.00/- |
| DAY CREAM | 360.00/- |
| CHARCOAL PEEL-OFF MASK | 285.00/- |
| ANTI-AGEING NIGHT CREAM | 255.00/- |
| COMPLETE FAIRNESS CREAM | 200.00/- |
| INSTANT GLOW FACE PACK | 170.00/- |
| CLARIFYING FACE WASH | 170.00/- |
| BB CREAM SPF 30+ | 400.00/- |
| SUN DEFENSE SPF 30+ | 265.00/- |
| PURIFYING CLEANSER + TONER | 315.00/- |
| DAILY MOISTURISER | 290.00/- |
| VITAMIN C GEL CRÈME | 280.00/- |
| VITAMIN C FACIAL FOAM | 382.00/- |
| INSTA-GLOW FACIAL KIT | 700.00/- |
| CHERRY BLOSSOM BODY BUTTER | 360.00/- |
| FOOT CREAM | 165.00/- |
| ALOE CUCUMBER AQUAGEl | 315.00/- |
| HAND & BODY LOTION | 225.00/- |
| SOAP | 54.00/- |
| COMPLEXION BAR | 84.00/- |
| Creamy Cleansing Bar | 69.00/- |
| HAND WASH | 145.00/- |
| HAND CLEANSING GEL | 340.00/- |
| GERM PROTECTION SOAP | 63.00/- |
| Pulse Perfume Spray | 325.00/- |
| Arctic Perfume Spray | 325.00/- |
| Aura Perfume Spray | 325.00/- |
| Charisma Perfume Spray | 100.00/- |
| Blossom Perfume Spray | 100.00/- |
| Captive Perfume Spray | 100.00/- |
| RAPTURE deo for women | 205.00/- |
| ENCHANT BODY TALC | 65.00/- |
| ACTIVE deo for men | 215.00/- |
| FORCE FRESH BODY TALC | 65.00/- |
| Hair Spa | 405.00/- |
| HAIR CONDITIONER | 245.00/- |
| Hair Oil | 195.00/- |
| DEEP CLEANSE SHAMPOO | 190.00/- |
| DAILY CARE SHAMPOO | 190.00/- |
| MOISTURE RICH SHAMPOO | 190.00/- |
| KERATIN SMOOTHENING SHAMPOO | 210.00/- |
| ANTI HAIRFALL BOUNCE RESTORE SHAMPOO | 210.00/- |
| INSTA RELIEF CREAM | 150.00/- |
| Vestige Women Hygiene | |
| FOAMING INTIMATE WASH | 210.00/- |
| SANITARY NAPKIN | 290.00/- |
| PANTY LINERS | 175.00/- |
| Vestige Oral Care | |
| MOUTHWASH | 205.00/- |
| TOOTHPASTE | 80.00/- |
| WHITENING TOOTHPASTE | 150.00/- |
| MULTI-ACTION TOOTHBRUSH | 260.00/- |
| GANO TOOTHPASTE | 175.00/- |
| Vestige Home Care | |
| ULTRA SCRUB | 220.00/- |
| ULTRA WASH | 375.00/- |
| ULTRA SWAB | 215.00/- |
| Ultra Matic | 185.00/- |
| Ultra Guard | 128.00/- |
| Vestige Agri products | |
| AGRI GOLD | 600.00/- |
| AGRI NANOTEK | 750.00/- |
| AGRI HUMIC | 650.00/- |
| Agri82 | 381.00/- |
| AGRI-PROTEK | 760.00/- |
| AGRI MOSS | 380.00/- |
| AGRI-HUMIC GRANULES | 825.00/- |
| Agri Aquagel | 2000.00/- |
| Vestige Mach-Drive | |
| MACH-DRIVE NANO ENERGIZER | 1700.00/- |
| Vestige Product for Men | |
| FACE WASH | 270.00/- |
| DEODORANT | 300.00/- |
| BATHING BAR | 140.00/- |
Also Download
- Vestige Product Catalogue Hindi
- Vestige Product Catalogue Bengali
- Vestige Product Catalogue Marathi
- Vestige Product Catalogue Tamil
- Vestige Product Catalogue Telugu
- Vestige Product Catalogue Urdu
- Vestige Product Catalogue Odia.